In [2]:
from scipy import signal
from scipy import ndimage
import matplotlib.pyplot as plt
import numpy as np
import os
from scipy import misc
from sklearn.cluster import KMeans
import seaborn as sns
from numpy import linalg as la
from math import floor
from ipywidgets import interact, interactive, fixed, interact_manual
from ipywidgets import FloatSlider
from ipywidgets import IntSlider
plt.rcParams['figure.figsize'] = (10, 10)
from mpl_toolkits import mplot3d

Página principal

Por Jerónimo Aranda.

Ver y pensar

Jerónimo Aranda

Introducción

Los humanos procesamos información visual de formas casi milagrosas y en tiempo real.

  • Ajustamos contraste
  • Ajustamos brillo
  • Leémos
  • Reconocemos objetos y caras.

¿Qué resolución ve el ojo humano?

Dejando por un lado la explicación neurológica, intentemos acercarnos a la comprensión de la visión desde el procesamiento de información.

Definiciones

Para acercarnos como buenos matemáticos a experiencias visuales, es necesario conceptualizar y abstraer de mejor forma estos objetos. Comencemos con definir $img(x,y)$ como una imagen en blanco y negro.

Sea $A =[0,m]$ x $[0,n] \in \mathbb{R}^2$, definamos una imagen como una función $img(x,y)$ de la siguiente forma :

$$img\colon \begin{array}{>{\displaystyle}l} A \rightarrow \mathbb{R} \\ (x,y)\mapsto img(x,y) \in [0,1] \end{array} $$

Es decir a cada una de las posiciones $(x,y)$ le corresponderá un tono de la escala de grises que se encuentra abajo.

In [109]:
sns_plot=sns.palplot(sns.color_palette("Greys",20))

Esta correspondencia pudiera darse con cualquier otra paleta de colores.

Ejemplo de imagen en blanco y negro

Dada la naturaleza continua de nuestro lienzo $A$, podemos suponer las posibles problemáticas que se presentan cuando una computadora intenta procesar una imagen. Para esto discretizaremos nuestra imagen con una nueva definición:

Nuestro imagen $img$ será una matriz real de $m*n$ en la que a cada una de sus entradas le corresponderá un valor entre cero y uno, es decir:

$$img(i,j)\in [0,1] $$

Por ejemplo, supongamos $m,n=50$ y elijamos valores aleatorios para cada $img(i,j)$:

In [53]:
img=np.random.random((500,500))
ax=plt.imshow(img,cmap='Greys')

Veamos la misma imagen codificada con una paleta distinta:

In [132]:
sns_plot=sns.palplot(sns.color_palette("viridis",20))
In [54]:
ax=plt.imshow(img,cmap='viridis')

Imágenes a color

Para extender la noción de imagen en blanco y negro a una a color, necesitamos extender nuestra matriz de $m*n$ a un tensor, o arreglo multidimensional con dimensiones $m*n*3$, en la que cada nivel de la 3era dimensión determina cada uno de los canales rojo, verde y azul.

$$img(i,j) = (r,g,b)$$

Con definición continua:

Sea $A =[0,m]$ x $[0,n] \in \mathbb{R}^2$, definamos una imagen a color como una función $img(x,y)$ de la siguiente forma :

$$img\colon \begin{array}{>{\displaystyle}l} A \rightarrow \mathbb{R}^3 \\ (x,y)\mapsto img(x,y) =\begin{bmatrix}r(x,y) \\ g(x,y) \\ b(x,y)\end{bmatrix} \end{array} $$

donde $r,g,b \in [0,1].$

In [3]:
def f(R,G,B):
    sns.palplot([R,G,B])
    return (R,G,B)
interact(f, R=FloatSlider(min=0, max=1, step=.05, value=.6,continuous_update=False),G=FloatSlider(min=0, max=1, step=.05, value=0.1,continuous_update=False),B=FloatSlider(min=0, max=1, step=.05, value=.4,continuous_update=False));
  • $(0,0,0)$ es negro.
  • $(1,1,1)$ es blanco.
  • cada $e_i$ corresponde a uno de los colores rojo, verde y azul.

Es importante mencionar que existen muchos otras abstracciones del color como CMYK,HSV and HSL, CIELAB.

Ejemplo imagen a color

In [5]:
plt.rcParams['figure.figsize'] = (20, 10)
In [6]:
import imageio
img=imageio.imread('../../../../Scripts/E1D73264-0143-42C7-B511-562343FB6D27.jpg')
ax=plt.imshow(img)
In [46]:
img[0,0,:]
Out[46]:
array([ 0,  9, 40], dtype=uint8)
In [123]:
plt.rcParams['figure.figsize'] = (10,8)

Canales R,G y B.

In [125]:
fig, axs = plt.subplots(3)
axs[0].imshow(img[:,:,0],cmap='Reds_r')
axs[1].imshow(img[:,:,1],cmap='Greens_r')
axs[2].imshow(img[:,:,2],cmap='Blues_r')
plt.show()

Derivada de una imagen

Recordando la primera definición.

Sea $A =[0,m]$ x $[0,n] \in \mathbb{R}^2$, definamos una imagen como una función $img(x,y)$ de la siguiente forma :

$$img\colon \begin{array}{>{\displaystyle}l} A \rightarrow \mathbb{R} \\ (x,y)\mapsto img(x,y) \in [0,1] \end{array} $$

Parece plantear inmediatamente la posibilidad de derivar. Esto está implementado por un filtro Sobel.

Filtro Sobel

Sea $img$ nuestra imagen, ($*$) la operación convolución entonces $G_x, G_y$ aproximan el gradiente en cada dirección:

$$\mathbf{G_x} = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix} * img \quad \mbox{y} \quad \mathbf{G_y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} * img $$

Y $G$ aproximará la magnitud del gradiente: $$\mathbf{G} = \sqrt{ \mathbf{G_x}^2 + \mathbf{G_y}^2 }$$

Leamos una imagen en blanco y negro.

In [12]:
plt.rcParams['figure.figsize'] = (8,8)
In [47]:
import imageio
img = imageio.imread('../../../../Scripts/C712DD03-E345-459E-928F-A9949A247E75-1000.jpg', as_gray=True)
ax=plt.imshow(img,cmap='Greys_r')
In [71]:
img[0,0]
Out[71]:
99.788

Derivemos aplicando el filtro sobel

In [50]:
from scipy import ndimage, misc
derivada=ndimage.sobel(img)
plt.imshow(derivada,cmap='Greys')
Out[50]:
<matplotlib.image.AxesImage at 0x1c1c0ef4e0>

Veamos el filtro sobel con imágenes a color

In [52]:
img = imageio.imread('../../../../Scripts/C712DD03-E345-459E-928F-A9949A247E75-1000.jpg')
derivada=ndimage.sobel(img)
plt.imshow(derivada)
Out[52]:
<matplotlib.image.AxesImage at 0x1c1d2950b8>
In [28]:
fig, axs = plt.subplots(3)
axs[0].imshow(derivada[:,:,0],cmap='Reds_r')
axs[1].imshow(derivada[:,:,1],cmap='Greens_r')
axs[2].imshow(derivada[:,:,2],cmap='Blues_r')
plt.show()

La media de varias imágenes

Supongamos que tenemos $k$ imágenes a color de $m*n$.

Definamos la media como:

$$\bar{img}= \frac{\sum_{i=1}^{k} img_{i}}{k}$$

Sin embargo recuerden que $img_{i}$ es un tensor, es decir, si analizamos el promedio en cada pixel tenemos:

$$\bar{img}(i,j)= \frac{\sum_{l=1}^{k} img_{l}(i,j)}{k}=\frac{\sum_{l=1}^{k} \begin{bmatrix}img_l(i,j,1) \\ img_l(i,j,2) \\ img_l(i,j,3)\end{bmatrix}}{k} $$

Instalación Cara a Cara

Formas de codificar información en visualizaciones:

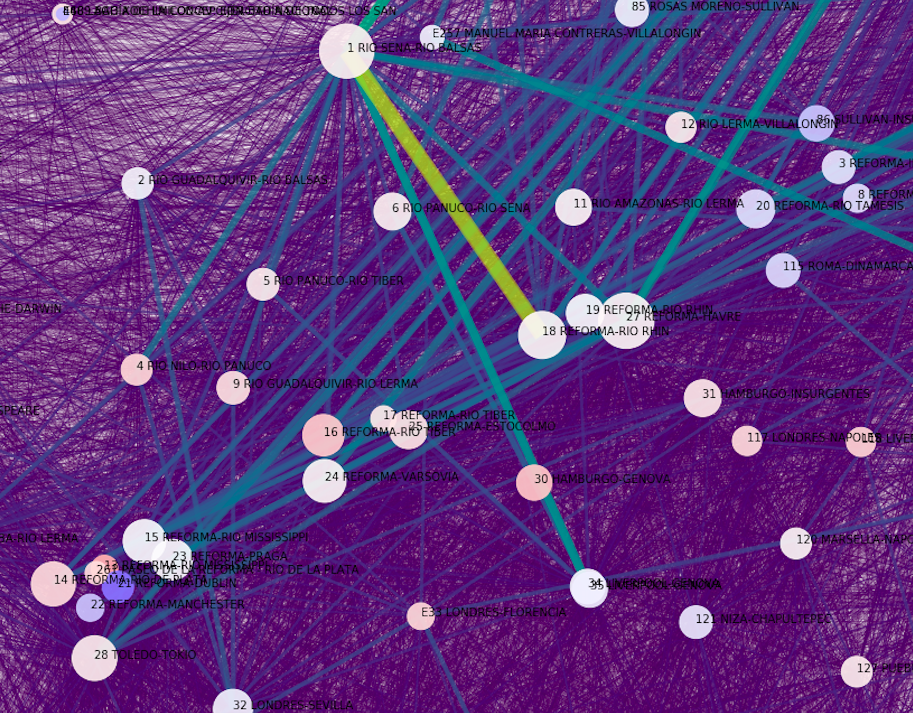
Ejemplos de paletas de color

Paleta secuenciales:

In [135]:
sns_plot=sns.palplot(sns.color_palette("inferno",20))

Paleta divergente:

In [52]:
sns_plot=sns.palplot(sns.color_palette("coolwarm",20))

Paleta categorica:

In [59]:
sns.palplot(sns.color_palette("hls", 20))

Conclusiones

  • El procesamiento de información visual se basa en conceptos matemáticos de campos diversos.

  • Python presenta herramientas bastante accesibles para comenzar a trabajar estos conceptos.

  • Las buenas visualizaciones permiten transformar conceptos abstractos o grandes cantidades de datos en información accesible al cerebro a 10 millones de bits por segundo.

Gracias

Página principal

Por Jerónimo Aranda.